Let me give you few simple questions. Answer them.
Are the consequences of detecting False Negatives are Highly severe?
If the answer is yes, Choose Recall.
If not ask again,
Are the consequences of detecting False Positives are Highly severe?
Now if question to this answer is yes, go with Precision.
Ok let’s dive a little bit by taking examples.
Predicting whether or not a patient has a tumor.
In this example,
- Detecting False Negatives is said to occur when the patient has Tumor BUT the model didn’t detected it. Now this case has very high Consequences. Since we didn’t detected the tumor, doctor will not the carry out necessary treatment. Fatal.
- But False Positives are not really our concern. Why? Say, the model detected a tumor, which in reality doesn’t actually exist. The patient will still be safe as other diagnosis might reveal the prediction was incorrect and no more treatment is required. No problem.
That’s why go for Recall.
Recall / True Positivity Rate / Sensitivity / Probability of Detection
What fraction of all positive instances does the classifier correctly identifies as positive.
\[\frac{\text{True Positive}}{\text{True Positive + False Negative}}\]
Classifying a good Candidate for a job
In this example,
- Detecting a False Positive occurs when model classifies a not so good candidate to be absolutely perfect for the job position. This has very high consequences for the recruitor as it increase the time for the recruitment process to complete.
- Candidates that are good enough for the position but are classified Incapable i.e. False Negatives, might not be able to reach upto interview. But if we see from Recruitor’s point of view, this will save time.
Here we would go with Precision.
Precision
For what fraction of positive predictions are correct.
\[\frac{\text{True Positive}}{\text{True Positive + False Positive}}\]
In the last example you might think it might be incorrect to discard perfectly good cadidates. Yeah you are right. But from the recruitor’s viewpoint the time is precious for him/her, and doesn’t justify interviewing a poor candidate.
Well that’s where we arrive at Precision/Recall Trade-off. Usually we prefer to use precision when the end result is to be used by end-user or customer facing applications (as they remember failures).
Precision/Recall Trade-off
As seen previously we actually needed both Precision and Recall to be high. We don’t want to waste time interviewing an incapable candidate BUT at the same time let go a perfectly acceptable or may be Perfect candidate.
Unfortunately You can’t have both; increasing precision reduces recall, and vice versa. This is called Precision/recall trade-off.
Plotting Recall and Precision against thresholds gives you way to select a good precision/recall trade-off threshold.
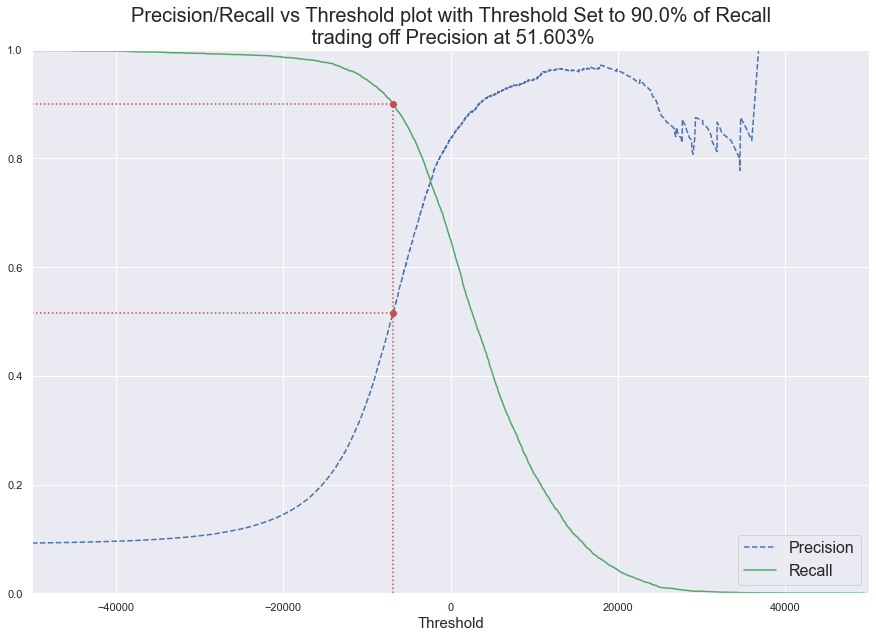
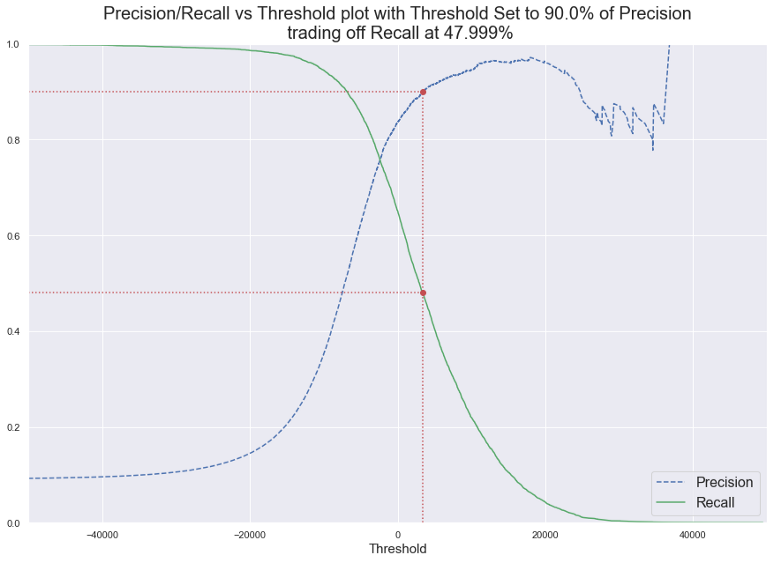
In case you were wondering how I plotted this, here is the code:
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import precision_recall_curve
# First you need to get the precisions, recalls, thresholds for your classifier.
y_scores = cross_val_predict(classifier, X_train, y_train, cv=3, method='decision_function')
precisions, recalls, thresholds = precision_recall_curve(y_train, y_scores)def plot_precision_recall_vs_threshold(precisions, recalls, thresholds, metric_name=None, metric_perc=None):
plt.figure(figsize=(15, 10))
plt.plot(thresholds, precisions[:-1], 'b--', label='Precision')
plt.plot(thresholds, recalls[:-1], 'g-', label='Recall')
plt.xlabel('Threshold', fontsize=15)
plt.axis([-50000, 50000, 0, 1])
plt.legend(loc='best', fontsize=16)
if metric_name=='precision':
metric = precisions
tradedoff_metric = recalls
tradedoff_metric_name = 'Recall'
# tradedoff metric & threshold at percentage metric we want.
tradedoff_atperc_metric = tradedoff_metric[np.argmax(metric >= metric_perc)]
threshold_atperc_metric = thresholds[np.argmax(metric >= metric_perc)]
elif metric_name == 'recall':
metric = recalls
tradedoff_metric = precisions
tradedoff_metric_name = 'Precision'
# tradedoff metric & threshold at percentage metric we want.
tradedoff_atperc_metric = tradedoff_metric[np.argmax(metric <= metric_perc)]
threshold_atperc_metric = thresholds[np.argmax(metric <= metric_perc)]
else:
return
# Draw the threholds, red dotted vertical line
plt.plot([threshold_atperc_metric, threshold_atperc_metric], [0., metric_perc], "r:")
# Draw the two horizontal dotted line for precision and recall
plt.plot([-50000, threshold_atperc_metric], [metric_perc, metric_perc], "r:")
plt.plot([-50000, threshold_atperc_metric], [tradedoff_atperc_metric, tradedoff_atperc_metric ], "r:")
# Draw the two dots
plt.plot([threshold_atperc_metric], [metric_perc], "ro")
plt.plot([threshold_atperc_metric], [tradedoff_atperc_metric], "ro")
plt.title("Precision/Recall vs Threshold plot with Threshold Set to {}% of {}\n trading off {} at {:.3f}%".format(
metric_perc*100,
metric_name.capitalize(),
tradedoff_metric_name,
tradedoff_atperc_metric*100), fontsize=20)
plt.show()
return threshold_atperc_metric
threshold = plot_precision_recall_vs_threshold(precisions, recalls, thresholds, 'precision', 0.9)
Now you can just this threshold to give your prediction, like this:
In[1] y_scores = clf.decision_function([instance_from_test_set])
no_threshold = 0
y_some_prediction = (y_scores > no_hreshold)
y_some_prediction
Out[1] array([True])
In[2] # Threshold returned from plotting func
y_some_prediction = (y_score > threshold)
y_some_prediction
Out[2] array([False])Another way of select a good precision/recall trade-off is to plot precision directly against recall.
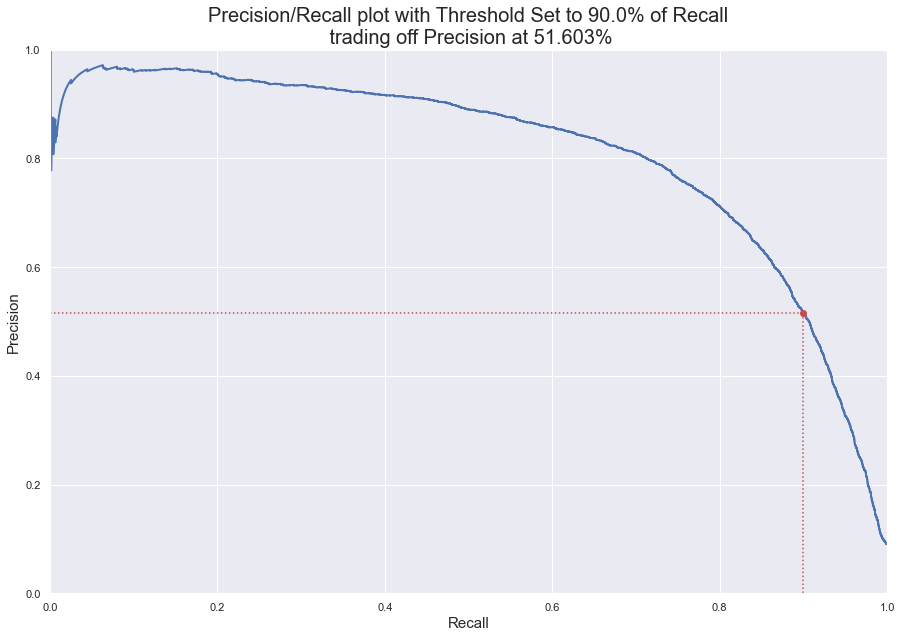
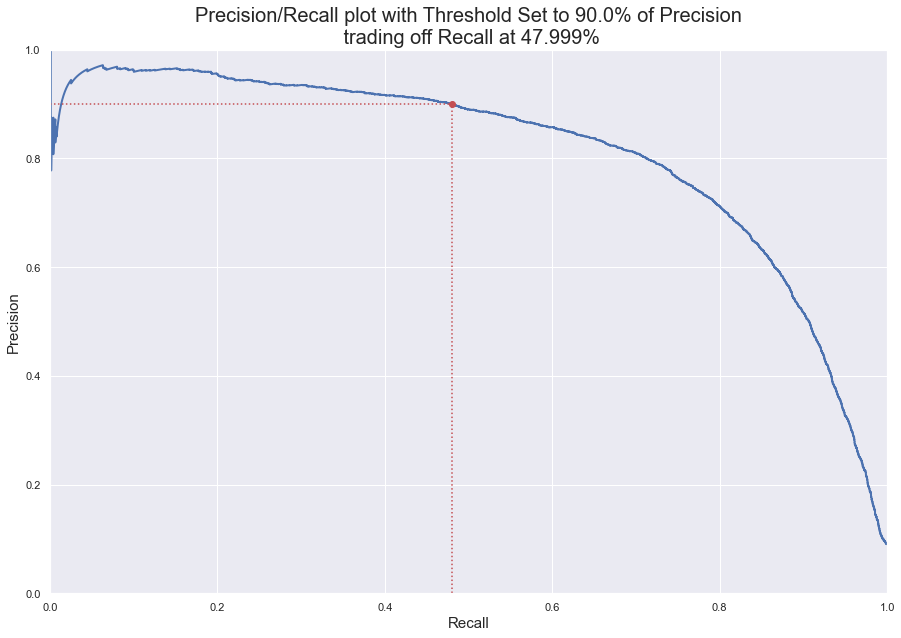
And again, you can generate this graph like this,
def plot_precision_vs_recall(precisions, recalls, metric_name=None, metric_perc=None):
plt.figure(figsize=(15, 10))
plt.plot(recalls, precisions, 'b-', linewidth=2)
plt.xlabel("Recall", fontsize=15)
plt.ylabel("Precision", fontsize=15)
plt.axis([0, 1, 0, 1])
if metric_name=='precision':
# tradedoff recall & threshold at percentage precision we want.
recall_atperc_precision = recalls[np.argmax(precisions >= metric_perc)]
threshold_atperc_precision = thresholds[np.argmax(precisions >= metric_perc)]
plt.plot([recall_atperc_precision, recall_atperc_precision], [0., metric_perc], 'r:')
plt.plot([0., recall_atperc_precision], [metric_perc, metric_perc], "r:")
plt.plot([recall_atperc_precision], [metric_perc], 'ro')
plt.title("Precision/Recall plot with Threshold Set to {}% of {}\n trading off Recall at {:.3f}%".format(
metric_perc*100,
metric_name.capitalize(),
tradedoff_atperc_metric*100), fontsize=20)
plt.show()
return threshold_atperc_precision
elif metric_name == 'recall':
# tradedoff precision & threshold at percentage recall we want.
precision_atperc_recall = precisions[np.argmax(recalls <= metric_perc)]
threshold_atperc_recall = thresholds[np.argmax(recalls <= metric_perc)]
plt.plot([0., metric_perc],[precision_atperc_recall, precision_atperc_recall], 'r:')
plt.plot([metric_perc, metric_perc],[0., precision_atperc_recall], "r:")
plt.plot([metric_perc],[precision_atperc_recall], 'ro')
plt.title("Precision/Recall plot with Threshold Set to {}% of {}\n trading off Precision at {:.3f}%".format(
metric_perc*100,
metric_name.capitalize(),
precision_atperc_recall*100), fontsize=20)
plt.show()
return threshold_atperc_recall
else:
return
threshold = plot_precision_vs_recall(precisions, recalls, 'recall', 0.9)After We have got threshold (returned from the function), predictions are done just as same way as shown in code block above.