Reframing a Machine Learning Problem

There are two sides to every coin.

And the same can be said for a few machine learning problems. Not every regression problem (that you think) needs to be a regression. Careful consideration and perspective on the business of the problem can not only help develop a better model but also make an effective solution.

Reframing is a strategy to change the representation of the output of a machine learning problem.

For example, we could take a regression problem and frame it instead as a classification problem (or vice versa).

Every machine learning problem begins with Scoping.

Scoping involves framing the problem, deciding the scope of the project, and who is going to use it by thinking from the user’s perspective. This can involve asking questions like:

Is this a supervised problem or unsupervised?
Who is the end-user we are catering to?
Is the end product critical to human life/property?
What amount of error is acceptable?

Suppose, we want to use Linear Regression to determine the staffing requirements of a Hospital, based on Operation Hours per Month of the hospital. This variable depends on independent variables of our dataset, such as the number of x-rays per month, number of occupied bed-days per month, and/or average length of patient's stay per month.

So this seemingly easy task looks to be a regression task since Operation Hours per Month is a continuous variable. As we start to build our regression model, we find that this task is harder than it sounds. The operation hours increases for the same set of feature, maybe because of acute illness during a particular period of the year, or due to some other inconsistencies. Our predicted operation hours can be off by (say) 10 hours. But this won't really affect the staffing requirements too much.

Perhaps we can reframe our machine learning objective in a way that improves performance.

The problem here is predicting the operation hours is probabilistic. Instead of trying to predict this variable as a regression task, we can frame the objective as a classification task.

Breaking the real-valued dependent variable into equal-sized bins/categories.

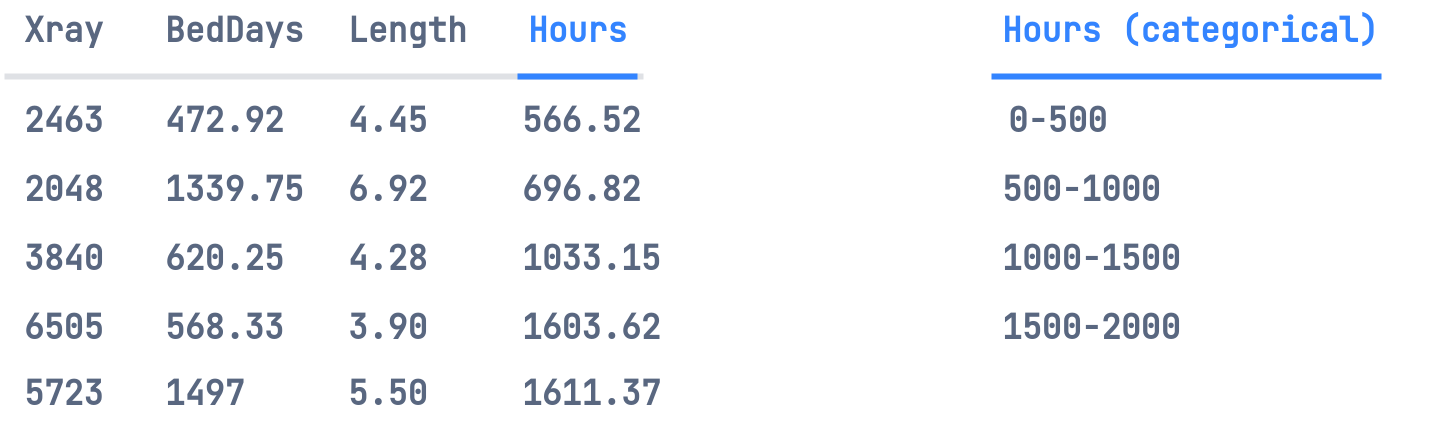
We'll then one-hot these categories and create a multiclass classification model that'll model the discrete probability distribution.

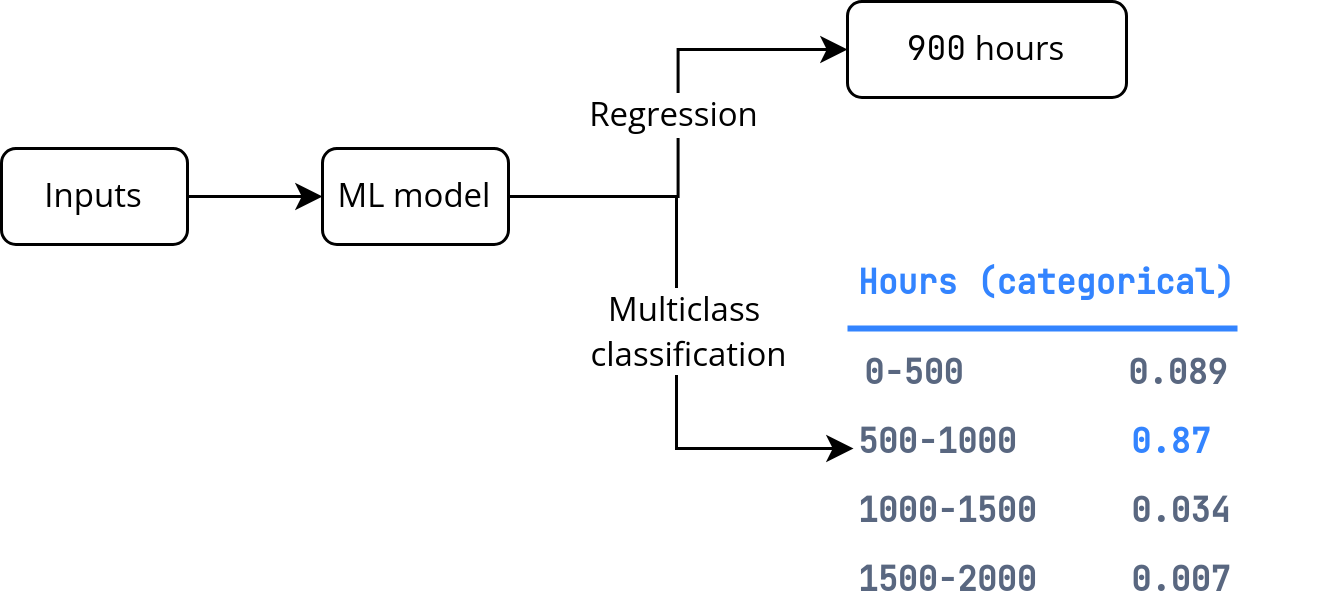
Of course, we need buckets to be much more fine-grained. But this is just for illustration purposes.

The classification approach allows the model to capture the probability distribution of operation hours at different discrete ranges instead of having to choose the mean of the distribution.

This comes advantageous when:

Variable does not exhibit a typical bell curve (maybe a tweedie distribution).
When the distribution is bimodal (a distribution with two peaks), or even when it is normal but with a large variance.
When the distribution is Normal but with a large variance

Why does it work?

We are changing the objective of the model to learn a continuous value to learning a discrete probability distribution; At the cost of loss of precision, but in turn, we gain the expressiveness of a full probability density function (PDF).

An added advantage of this classification framing is that we obtain posterior probability distribution of our predicted values, which provides, which provides more nuanced information.

Trade-Offs and Alternatives

Another approach is multitask learning which combines both tasks (classification and regression) into a single model using multiple prediction heads, but be aware of the risk of introducing label bias due to limitations of the dataset.

Reframing a regression problem is a very good way to capture uncertainty. Other ways to capture uncertainty is to carry out quantile regression.

For example, instead of predicting just the mean, we can estimate the conditional 10th, 20th, 30th, ..., 90th percentile of what needs to be predicted. Quantile regression is an extension of linear regression. Reframing on the other hand, can worrk with more complex machine learning models.

Precision of prediction

As seen in the previous example, we traded-off the precision to gain the expressiveness of discrete Probability Distribution Fuction (PDF). If we need were needed to be more precise then we would need to increase the number of bins of our categorical model.

The sharpness of the PDF indicates the precision of the task as a regression. A sharper PDF indicates a smaller standard deviation of the output distribution while a wider PDF indicates a larger standard deviation and thus more variance.

For a sharp density function, stick with a regression model.

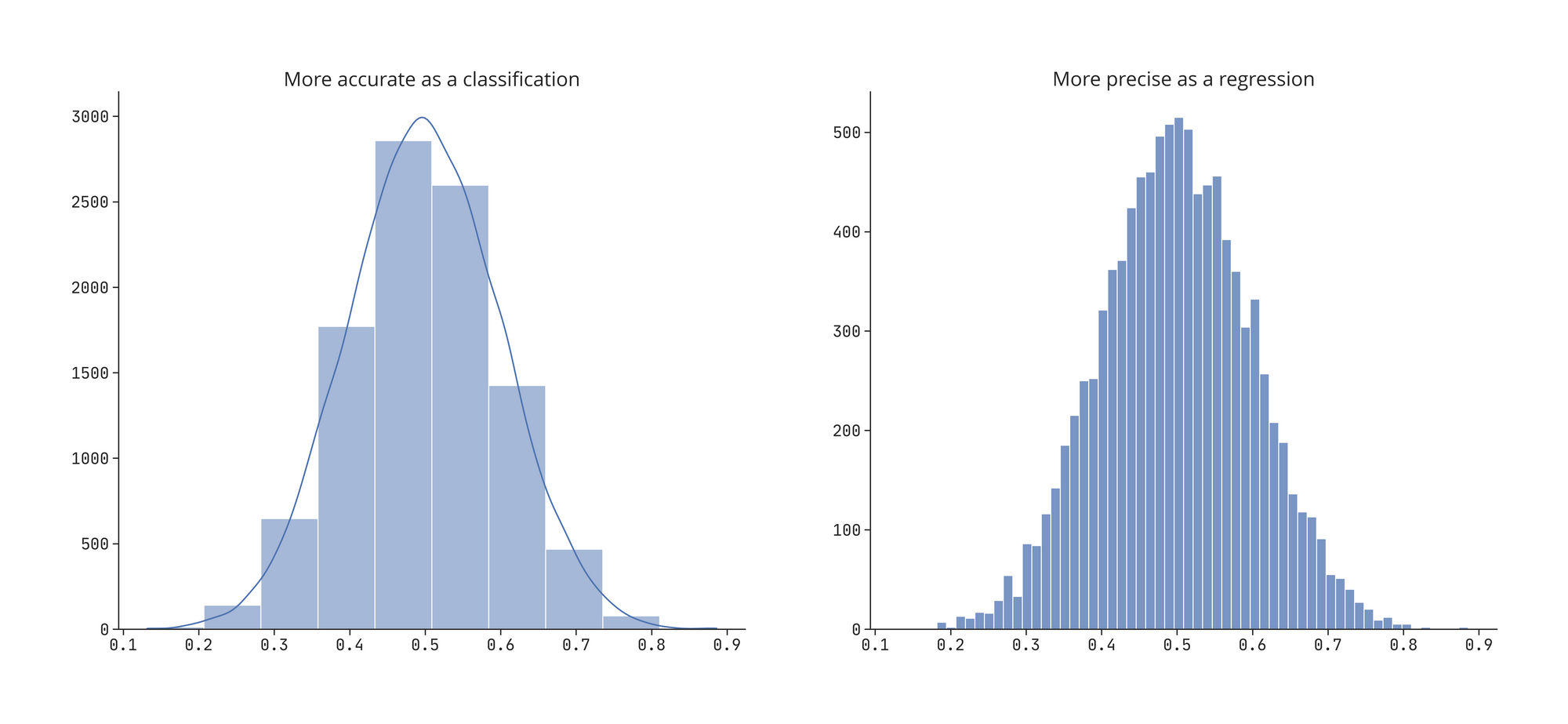
The precision of the regression is indicated by the sharpness of the probability density function for a fixed set of input values.

We can get the same plot on the the left by bucketizing the feature that was in plot on the right.

Also don't get confused between the concept of accuracy and precision:

Accuracy is how close measurement is to the true value.

Precision is how close measurements are (of the same item) are to each other.

Reframing as a way to limit the prediction range

A lot of times the prediction range is a real-valued variable. Simply using a dense layer with one neuron may throw the prediction output beyond the acceptable/interpretable range.

Reframing can come to the rescue here.

To limit the prediction range, make the activation function of the last-but-one layer a sigmoid function (often associated with classification) so that it is in the range [0, 1] and have the last layer scale these values to the desired range:

MIN_Y = 3
MAX_Y = 20
input_size = 10

inputs = keras.layers.Input(shape=(input_size,))
h1 = keras.layers.Dense(20, 'relu')(inputs)
h2 = keras.layers.Dense(1, 'sigmoid')(h1) # a sigmoid layer
output = keras.layers.Lambda(
	lambda y: (y*(MAX_Y-MIN_Y) + MIN_Y)
    )(h2) # a custom layer for scaling
model = keras.Model(inputs, output)

Since the output is a sigmoid, the model will never actually hit the minimum or maximum of the range, just get close to it.

Label bias

Neural networks based recommendation systems framed as regression or classification models are far more advantageous than matrix factorization as they can incorporate many more additional features outside of just the user and item embeddings learned in matrix factorization.

However, framing the objective as a classification problem (viewer will click or not) can lead to recommendation system prioritizing clickbait.

In that scenario, it is better to reframe the objective into a regression problem predicting the fraction of the video that will be watched, or the video watch time or even predict the likelihood that a user will watch at least half the video clip.

Multitask Learning

Instead of reframing the task to be either regression or classification, we can even try out both, referred as Multitask Learning.

Multitask Learning refers to any machine learning model in which more than one loss function is optimized.

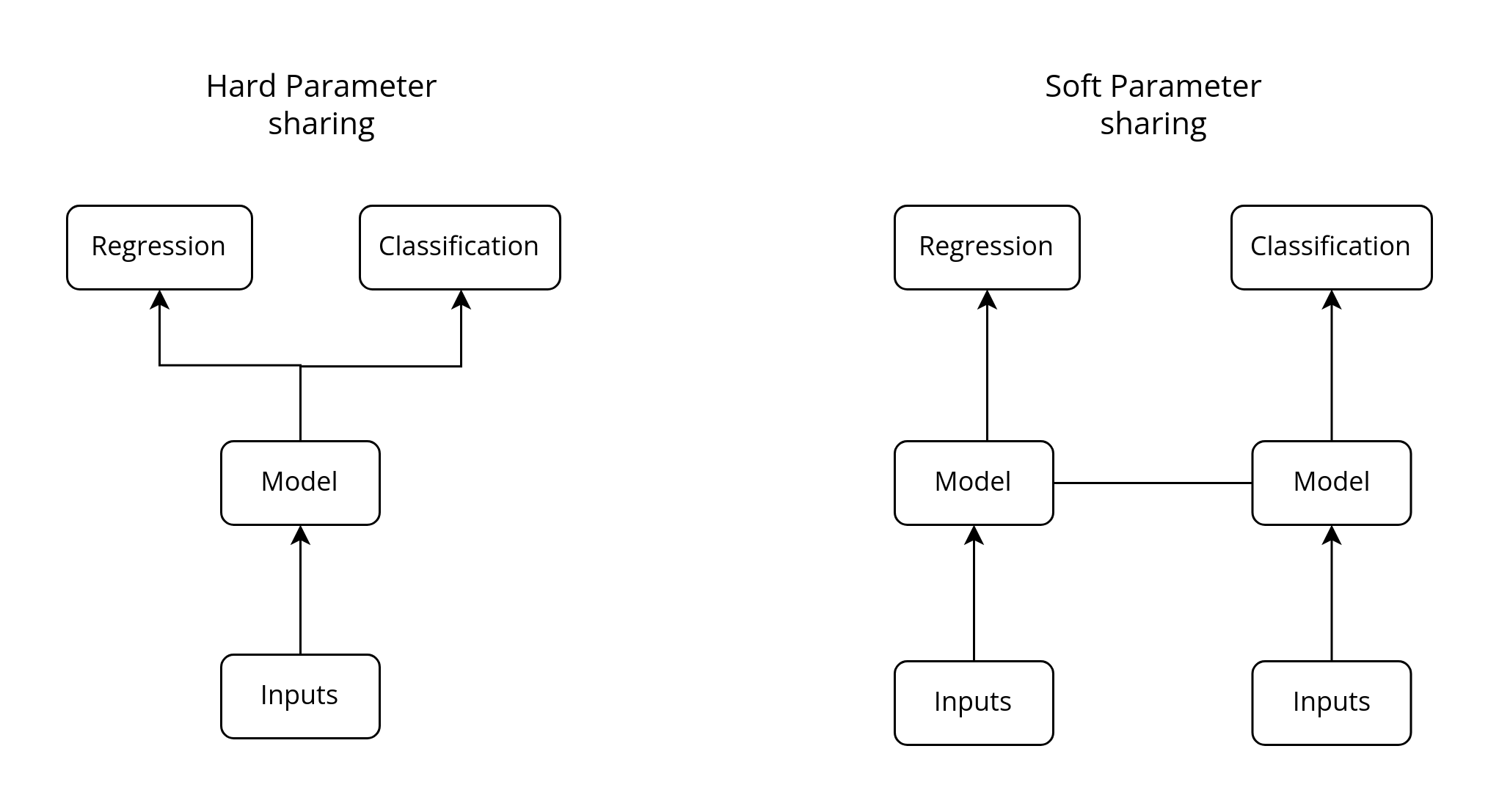
The two most common forks of multitask learning in neural networks are through:

Hard parameter sharing – when the hidden layers of the model are shared between all the output tasks.
Soft parameter sharing – when each label has its own neural network with its own parameters, and the parameters of the different models are encouraged to be similar through some form of regularization.